前端中的变换矩阵

在一票教你如何制作立方体的教程之后，在张鑫旭生动的类比讲解¹²之后，我还想重提一次前端中的变换矩阵——它被挖掘得远远不够。
本文里，让我们从W3C标准和浏览器等新角度来重新理解变换矩阵。

变换矩阵的综合应用

在开始前，我们不妨看动画库bouncejs来热身一下。

一个动画如果要给人带来愉悦、动人甚至是惊艳的感觉，它首先要足够贴近我们的经验，否则我们理解不了动画过程；其次，它还要有充沛的细节，否则会显得单调乏味。
bouncejs这个库就同时做到了这两点。

我们知道CSS3中的时间函数其实是非常残缺的，它最复杂也不过是生成一个有四个参数的三次贝塞尔曲线，还远远不够我们对于动画细腻程度的追求。如果细窥bouncejs的实现，我们会发现它用到了线性的时间函数，而在keyframes中表达动画细节，用到了一大堆matrix3d：

@keyframes animation{
    /* ... */
    21.32% { transform: matrix3d(2.196, 0, 0, 0, 0, 2.069, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1); }
    24.32% { transform: matrix3d(2.151, 0, 0, 0, 0, 1.96, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1); }
    /* ... */
}

如何实现：我们想要的动画中的回弹、硬直等效果如何拆解为这些matrix3d的呢？
背后机制：这些matrix3d是如何组合成我们想要的动画效果的呢？

变换矩阵的用法

先来看看变换矩阵在各处的表现形式吧。

CSS中的变换矩阵

也许是我们第一次接触变换矩阵的地方。

.selector {
    transform: matrix(a, b, c, d, e, f);
    transform: matrix3d(m11, m12, m13, m14, m21, m22, m23, m24, m31, m32, m33, m34, m41, m42, m43, m44);
}

SVG中的变换矩阵

SVG作为可缩放矢量图形，它局限于2D坐标中，因此它只有二维变换：

<g transform="matrix(a, b, c, d, e, f)"></g>

注意，由于SVG没有transform-origin属性，因此需要自己用translate来模拟。
可参考:

DEMO #1
SVG相对中心翻转和相对中心旋转的实现
实现方式：三个transform的嵌套。

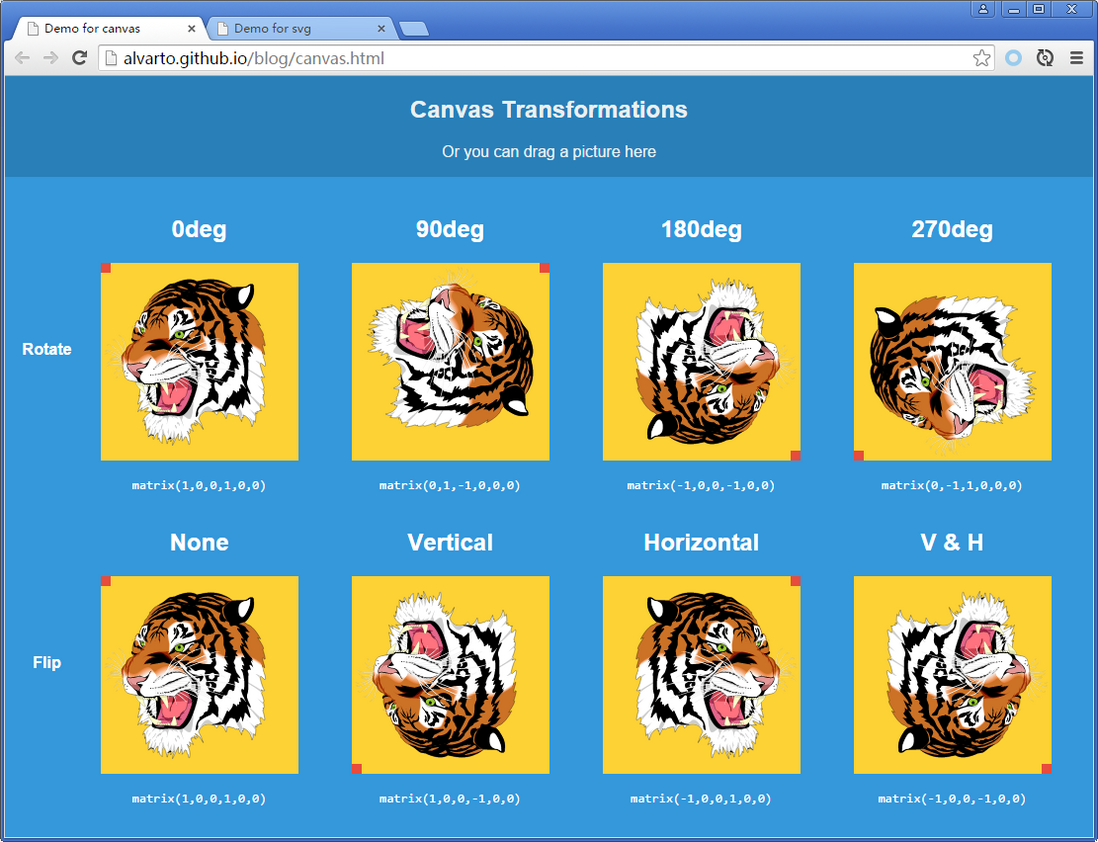
CANVAS中的变换矩阵

首先是2d Context中的变换矩阵。

var context = canvas.getContext("2d");
context.transform() /*与之前的矩阵值累乘*/
context.setTransform() /*不与之前的矩阵值累乘*/

它跟SVGMatrix接口一样，因此也不支持transform-origin，需要用translate模拟。
可参考:

DEMO #2
Canvas相对中心翻转和相对中心旋转的实现
实现方式：三个transform的嵌套。

IE中的filter变换矩阵

一个遗留的接口，不做多介绍。
可见：张鑫旭：IE矩阵滤镜Matrix旋转与缩放及结合transform的拓展。

JS中的变换矩阵

DOM接口

我们可以用getComputedStyle来获取到相应的transform参数，获得的值是一个字符串。

window.getComputedStyle(dom).transform
window.getComputedStyle(dom).webkitTransform

矩阵包装器

webkit浏览器和IE曾经支持私有的包装器（WebkitCSSMatrix和MSCSSMatrix），可以在得到字符串以后协助我们做一些矩阵运算,但目前已被浏览器废弃。
我们可以自己实现一个类似的包装器，可参考github: CSSMatrix。
此外，在THREE.JS中也存在包装器THREE.Matrix4。

数学中的变换矩阵

变换矩阵的实质为一组线性变换的系数矩阵。变换的目标为坐标。
系数矩阵的应用方式，在于其用于左乘点向量的齐次坐标。
当算出的齐次坐标值不为1的时候，需要完成齐次除法 homogeneous divide，使得第四个值为1，以算出最终的坐标值。

计算过程如下图：

最后，一个变换矩阵不仅仅是描述坐标点变换，其实也描述了坐标系变换（基变换）。

变换矩阵的乘法

需要注意的是，变换矩阵的乘法是不符合乘法交换律的。可参考：

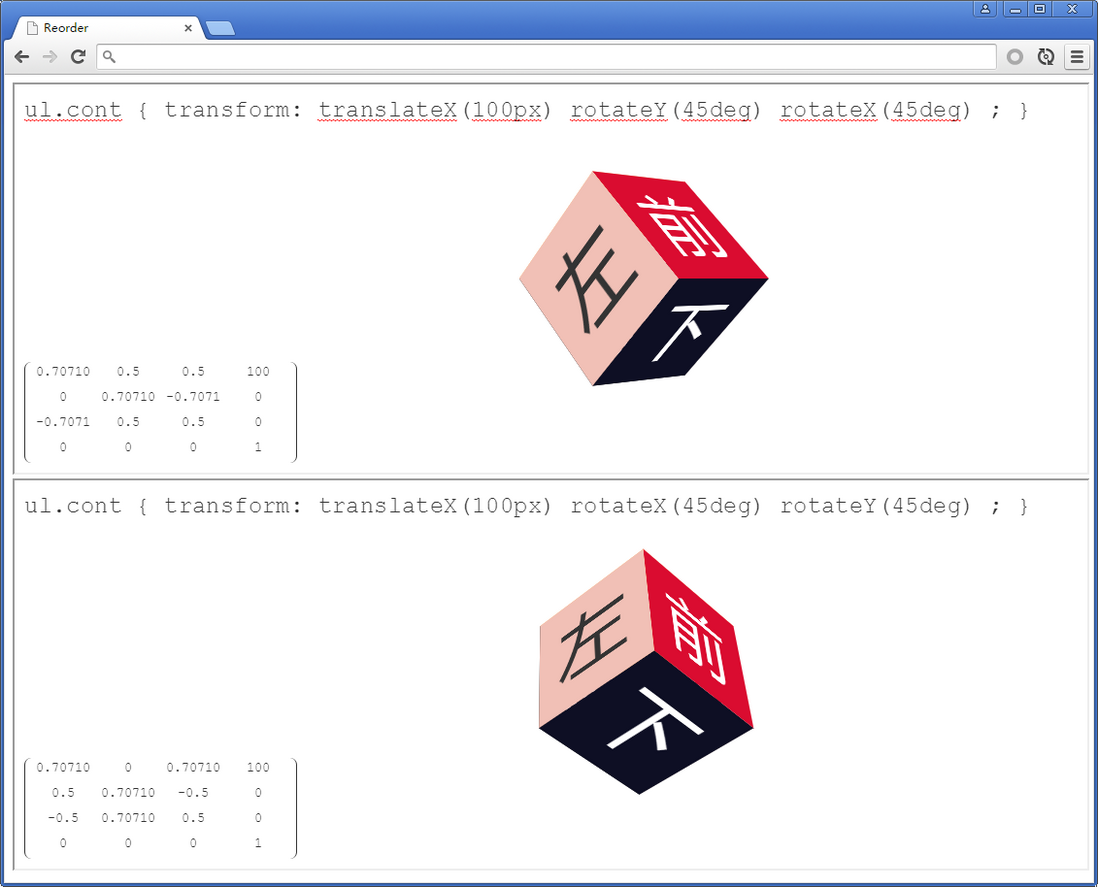
DEMO #3
重新排序变换矩阵/函数。
测试方法：改变上方或下方的transform中的rotateY和rotateX的顺序，比较他们的矩阵和显示效果

可见，交换律是不符合的。

一些特殊情况下，矩阵A乘以矩阵B正好等于矩阵B乘以矩阵A。

常规的例子是单位矩阵E左乘或右乘A，都将得到A。
一个很简单的理解：单位矩阵其实代表了x'=x、y'=y...的方程组的系数矩阵。

变换矩阵的局限性

再怎么变换，变换矩阵都是一个线性变换，无法将直线变成曲线。所以鱼眼之类的效果不能简单的用变换矩阵来完成。

标准中的变换矩阵

影响变换矩阵的属性

变换中心点：transform-origin

上文已有DEMO实例。变换中心点功能是由变换矩阵左乘坐标位移矩阵P，和右乘坐标位移矩阵的逆矩阵P^-1，来影响结果的：

变换透视：perspective、perspective-origin

从CSSTricks里面借一张图：

上图中眼睛位置相关的三个坐标可以借由这些属性调整：

• p：perspective

• 眼睛的x和y：perspective-origin

父子坐标系共享：transform-style

变换：transform

2d

• translate

• scale

• rotate

• skew

• matrix

3d

• translate3d

• scale3d

• rotate3d

• perspective

• matrix3d

如何算得最终变换矩阵

1. 计算变换矩阵

   1. 从单位矩阵开始

   2. 乘以transform-origin的坐标系变换矩阵

   3. 按照声明顺序，乘以每一个transform function其对应矩阵

   4. 乘以transform-origin的逆坐标系变换矩阵

2. 计算累计变换矩阵

   1. 对于该元素和3D渲染上下文根元素的每一个包含块，从单位矩阵开始

   2. 乘以其包含块上的perspective矩阵

   3. 乘以当前块相对其包含块的水平、垂直位移矩阵

3. 将累积变换矩阵乘以变换矩阵，得到最终变换矩阵

变换矩阵的动画

平常动画过程中，有两个概念：

1. Timing function 时间函数：由时间函数f得到插值比例。
   t=f(tNow, tTotal)
tNow：经过时间
tTotal：总时间

2. Interpolation：插值函数：由插值函数g得到最终的值。(多半是线性插值)
   s=g(t, xStart, xEnd)
t：插值比例
xStart：开始值
xEnd：结束值

对于变换矩阵，会采用线性的插值方式吗？请参考：

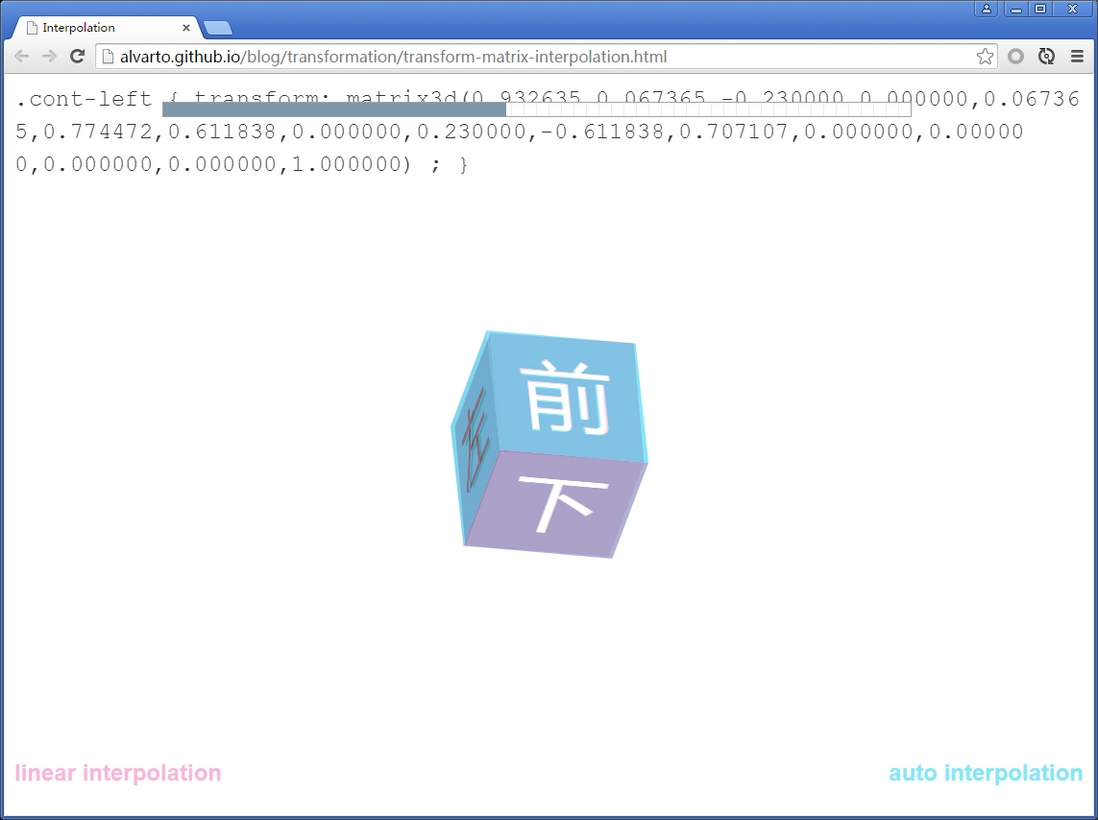
DEMO #4
矩阵的插值实验
实验方式：左边为用js实现的线性插值，右边为用animation实现的方法，起止皆为matrix。
测试方法：点击“combine”，然后再点击“play”。

可以由轮廓的不重合之处发现，线性的插值是不准确的插值方式。

根据标准，矩阵插值的方式是这样的：

1. Decomposing：将矩阵分解为多个子变换，并求得对应的向量。

   1. perspective

   2. translate

   3. quaternion（四元数）

   4. skew

   5. scale

2. 分别对各个子变换进行插值计算

   1. 四元数向量的插值方法为球面线性插值spherical linear interpolation

   2. 其它的子变换都通过简单的线性插值计算

3. Recomposing：插值结束以后，将各个子矩阵按顺序相乘，得到最终的矩阵。

   1. 单位矩阵

   2. 乘以perspective matrix

   3. 乘以translation matrix

   4. 乘以rotation matrix

   5. 乘以skew matrix

   6. 乘以scale matrix

浏览器中的变换矩阵

benchmark: transform matrix和transform function哪个更快

to be continued

Chrome中的变换矩阵

了解了数学中的相关概念，我们即可参考源码中变换矩阵的实现方式了。

SK_API::SkMatrix44

包含了对矩阵本身的定义、矩阵相关的数据类型和矩阵的基础计算。
这个类是矩阵相关的最基础的4*4的矩阵数据结构。

源码：

• SkMatrix44.h

• SkMatrix44.cpp

包含：

1. 一个SkMScalar类，根据编译选项可用于表示float或double；

2. set*()为设置当前矩阵为某变换对应的矩阵，而pre*()和post*()则为在某项变换之后或之前的变换操作，也可以理解为某个变换矩阵的左乘或右乘；

3. determinant()为求矩阵的行列式；

4. invert()求逆矩阵；

5. transpose()转置矩阵；

6. computeTypeMask()方法展示了如何通过计算得到一个变换矩阵是否包含如下变换：

   • 位移：translate

   • 伸缩：scale

   • 仿射：affine，包含旋转 rotate 和斜切 skew

   • 透视：perspective

gfx::transform

这个类映射到CSS中的transform声明。

源码：

• transform.h

• transform.cc

包含：

1. 2d、3d的构造函数、拷贝构造函数、一些运算符重载

2. 针对CSS中的各类声明方式，得到对应的变换。包括但不限于：
   Translate();
Translate3d();
Scale();
Scale3d();
RotateAboutXAxis();
RotateAbout();

3. 应用透视 perspective
   ApplyPerspectiveDepth()

4. 左乘和右乘
   PreconcatTransform();
ConcatTransform();

5. 对矩阵性质的判断
   IsScale2d()
IsApproximatelyIdentityOrTranslation()

6. 其他矩阵操作，如转置和得到逆变换
   GetInverse()
Transpose();

7. 矩阵插值操作
   Blend()

gfx::transform_util

包含变换相关的一些数学计算功能、除了矩阵以外的数据类型定义。

源码：

• transform_util.h

• transform_util.cc

包含：

1. 点类Point和矩形类Rect

2. DecomposedTransform矩阵插值过程中的类，包含各个变换相关的特征值向量：

   • 位移向量：translate[3]

   • 缩放向量：scale[3]

   • 斜切向量：skew[3]

   • 透视向量：perspective[4]

   • 四元数向量：quaternion[4]，用于旋转。不用常规的三变量表示方法是为了避免欧拉锁问题。

3. 一些辅助方法

   1. 由矩阵拆解为DecomposedTransform的方法DecomposeTransform()

   2. 方法BlendDecomposedTransforms()，由DecomposeTransform参与的插值方法

   3. 方法Slerp()，用于四元数的球面插值方法

   4. 得到三元向量的长度Length3()

   5. 向量点乘Dot()

   6. 将矩阵归一化Normalize()

   7. 应用变换中心的方法TransformAboutPivot