我们先看下最后的效果
实现思路
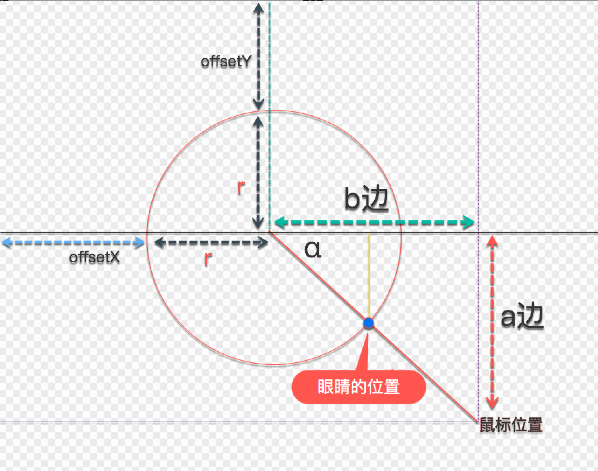
- 要实现眼睛随鼠标一起运动,我们必须先求出眼睛的坐标,也就是它的left和top值
- 为了取到left和top值,我们只要知道α角的内三角形的对边和邻边的长度即可
- 为了取到对边和邻边,我们只需要知道α角的弧度即可
- α角的弧度,我们可能通过图中a边和b边,再使用
arctan(a/b),即可求得 - a边的长度为:鼠标y轴的坐标 - (offsetY + r)
- b边的长度为:鼠标x轴的坐标 - (offsetX + r)
部分实现
计算offsetX和offsetY
// 旋转轨道的left和top值,也就是图中offsetX和offsetY
var wLeft = $('.wrap').offset().left
var wTop = $('.wrap').offset().top
// 旋转轨道的半径
var r = 12计算a边和b边的长度
// b边的长度
var diffX = ev.pageX - (wLeft + r)
// a边的长度
var diffY = ev.pageY - (wTop + r)计算α
// 弧度α
var deg = Math.atan(Math.abs(diffY) / Math.abs(diffX))计算内三角形的对边和邻边
// 内三角形的邻边
var x = Math.cos(deg) * r
// 内三角形的对边
var y = Math.sin(deg) * r计算出眼睛的left值和top值
var left = (r + x) + 'px'
var top = (r + y) + 'px'四象限角度问题
上面我们获取了left值和top值,但是这只限于0~90度,也就是第四象限是可以了,关于四象限,我们上一张图
当鼠标落在第三象限的时候,计算出来的角度应该是90~180度,我们得出:
deg = Math.PI - deg当鼠标落在第二象限的时候,计算出来的角度应该是180~270度,我们得出:
deg = Math.PI + deg当鼠标落在第一象限的时候,计算出来的角度应该是270~360度,我们得出:
deg = 2 * Math.PI - deg

**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。