JavaScript mathematical curve-equiangular spiral

Introduction

Following the Archimedes spiral , the equiangular spiral was discovered.

• Origin
• My GitHub

Introduction

Equiangular spirals are also called golden spirals or logarithmic spirals. In 1638, Descartes discovered equiangular spirals. Later, Jakob Bernoulli researched and discovered the characteristics of self-reconstruction of equiangular spirals. Jakob Bernoulli was very fascinated by spirals. As for his request to be inscribed on his tombstone, with the word "eadem mutata resurgo" ("Even if I change, I still remain the same"). In the end, Torricelli completed the work independently and found the length of the curve.

The origin of the name of the equiangular spiral is due to its characteristics: take any point A on the spiral, the straight line formed by this point and the pole of the polar coordinate, and the angle formed by the tangent of the point is a fixed value.

Formula description in polar coordinate system:

Formula description:

• r: the distance from the origin.
• a: Constant.
• b: constant.
• e: constant.
• θ: The angle to the x-axis.

Natural phenomena include:

• Nautilus shells resemble equiangular spirals.
• The seeds of the chrysanthemum are arranged in an equiangular spiral.
• Insects approach the light source in an equiangular spiral.
• The spiral arms of spiral galaxies are almost equiangular.
• The appearance of low pressure (tropical cyclones, extratropical cyclones, etc.) is like an equiangular spiral

draw

Use canvas to draw a curve. The coordinate system of the canvas is a Cartesian coordinate system, which requires a conversion.

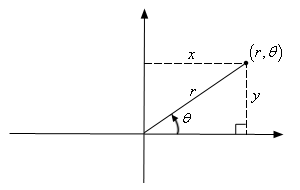
From the above figure, it can be seen that taking a point has the following mathematical conversion relationship:

x = rcos(θ)
y = rsin(θ)
θ = arctan(y/x)

Combined with the formula of the polar coordinate system, we can get:

This is the example , drawing the main logic code:

function draw() {
  let a = 0.1, b = 0.3, angle = 0;
  let x = 0, y = 0, points = [];
  const acceleration = 0.1, circleNum = 4;
  // 注意这里角度的递增，以 2 * Math.PI 为基准进行比较，控制画多少圈
  while (angle <= circleNum * 2 * Math.PI) {
    const anglePow = Math.pow(Math.E, b * angle);
    x = a * anglePow * Math.cos(angle);
    y = a * anglePow * Math.sin(angle);
    points.push([x, y]);
    angle = angle + acceleration;
  }
  // 实现把点绘制成线的方法
  line({ points: points});
}

Reference

• Golden spiral Wiki
• Logarithmic Spiral
• Equiangular Spiral
• Isometric spiral