引子
继等角螺线,接着尝试连锁螺线。
简介
在 阿基米德螺线 中提到的通用的公式,当 c = -2 时,就是连锁螺线,又称为 Lituus 曲线。Roger Cotes 在他的著作 《Harmonia Mensurarum》(1722) 中对该曲线进行了描述。Maclaurin 在 1722 年为曲线命名。
在极坐标系中公式描述:
公式说明:
- r :径向距离。
- a :常数。
- θ :极角。
绘制
用 canvas 绘制曲线,canvas 的坐标系是笛卡尔坐标系,需要做一个转换。
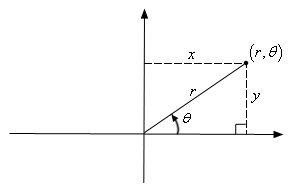
由上面的图可知取一个点有下面的数学转换关系:
x = rcos(θ)
y = rsin(θ)
θ = arctan(y/x)结合极坐标系公式可得:
这是示例,绘制主要逻辑代码:
function draw() {
let a = 100, angle = 0.1;
let x = 0, y = 0, points = [];
const acceleration = 0.1, circleNum = 20;
while (angle <= circleNum * 2 * Math.PI) {
const angleSqrt = Math.sqrt(angle);
x = (a / angleSqrt) * Math.cos(angle);
y = (a / angleSqrt) * Math.sin(angle);
points.push([x, y]);
angle = angle + acceleration;
}
// 实现把点绘制成线的方法
line({ points: points});
}


**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。