JavaScript mathematical curve-interlocking spiral

Introduction

Following the equiangular spiral , then try to interlock the spiral.

• Origin
• My GitHub

Introduction

The general formula mentioned in Archimedes spiral , when c = -2, is the interlocking spiral, also known as the Lituus curve. Roger Cotes described this curve in his book "Harmonia Mensurarum" (1722). Maclaurin named the curve in 1722.

Formula description in polar coordinate system:

Formula description:

• r: Radial distance.
• a: Constant.
• θ: Polar angle.

draw

Use canvas to draw a curve. The coordinate system of the canvas is a Cartesian coordinate system, which requires a conversion.

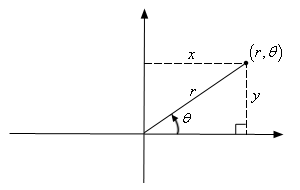
From the above figure, it can be seen that taking a point has the following mathematical conversion relationship:

x = rcos(θ)
y = rsin(θ)
θ = arctan(y/x)

Combined with the formula of the polar coordinate system, we can get:

This is the example , the main logic code is drawn:

function draw() {
  let a = 100, angle = 0.1;
  let x = 0, y = 0, points = [];
  const acceleration = 0.1, circleNum = 20;
  while (angle <= circleNum * 2 * Math.PI) {
    const angleSqrt = Math.sqrt(angle);
    x = (a / angleSqrt) * Math.cos(angle);
    y = (a / angleSqrt) * Math.sin(angle);
    points.push([x, y]);
    angle = angle + acceleration;
  }
  // 实现把点绘制成线的方法
  line({ points: points});
}

Reference

• Lituus Wiki
• Lituus Wolfram MathWorld
• Lituus Plane Curves
• Lituus