全文链接:http://tecdat.cn/?p=10175
最近我们被客户要求撰写关于Rasch的研究报告,包括一些图形和统计输出。
几个月以来,我一直对序数回归与项目响应理论(IRT)之间的关系感兴趣
在这篇文章中,我重点介绍Rasch分析。
最近,我花了点时间尝试理解不同的估算方法。三种最常见的估算方法是:
联合最大似然(JML)条件逻辑回归,在文献中称为条件最大似然(CML)。标准多层次模型,在测量文献中称为边际最大似然(MML)。阅读后,我决定尝试进行Rasch分析,生成多个Rasch输出。
相关视频
**
拓端
,赞15
例子
需要ggplot2和dplyr才能创建图表。
library(Epi) # 用于带对比的条件逻辑回归library(lme4) # glmerlibrary(ggplot2) # 用于绘图library(dplyr) # 用于数据操作数据。
raschdat1 <- as.data.frame(raschdat)CML估算
res.rasch <- RM(raschdat1)系数
coef(res.rasch)beta V1 beta V2 beta V3 beta V4 beta V51.565269700 0.051171719 0.782190094 -0.650231958 -1.300578876beta V6 beta V7 beta V8 beta V9 beta V100.099296282 0.681696827 0.731734160 0.533662275 -1.107727126beta V11 beta V12 beta V13 beta V14 beta V15
-0.650231959 0.387903893 -1.511191830 -2.116116897 0.339649394beta V16 beta V17 beta V18 beta V19 beta V20-0.597111141 0.339649397 -0.093927362 -0.758721132 0.681696827beta V21 beta V22 beta V23 beta V24 beta V250.936549373 0.989173502 0.681696830 0.002949605 -0.814227487beta V26 beta V27 beta V28 beta V29 beta V301.207133468 -0.093927362 -0.290443234 -0.758721133 0.731734150
# 使用回归
raschdat1.long$tot <- rowSums(raschdat1.long) # 创建总分c(min(raschdat1.long$tot), max(raschdat1.long$tot)) #最小和最大分数[1] 1 26raschdat1.long$ID <- 1:nrow(raschdat1.long) #创建IDraschdat1.long <- tidyr::gather(raschdat1.long, item, value, V1:V30) # 宽数据转换为长数据# 转换因子类型raschdat1.long$item <- factor(
raschdat1.long$item, levels = p
# 条件最大似然
回归系数item1 item2 item3 item4 item50.051193209 0.782190560 -0.650241362 -1.300616876 0.099314453item6 item7 item8 item9 item100.681691285 0.731731557 0.533651426 -1.107743224 -0.650241362item11 item12 item13 item14 item150.387896763 -1.511178125 -2.116137610 0.339645555 -0.597120333item16 item17 item18 item19 item200.339645555 -0.093902568 -0.758728000 0.681691285 0.936556599item21 item22 item23 item24 item250.989181510 0.681691285 0.002973418 -0.814232531 1.207139323item26 item27 item28 item29 -0.093902568 -0.290430680 -0.758728000 0.731731557
请注意,item1是V2而不是V1,item29是V30。要获得第一个题目V1的难易程度,只需将题目1到题目29的系数求和,然后乘以-1。
sum(coef(res.clogis)[1:29]) * -1[1] 1.565278# 再确认两个模型是否等效res.rasch$loglik #Rasch对数似然[1] -1434.482# 条件逻辑对数似然,第二个值是最终模型的对数似然res.clogis$loglik[1] -1630.180 -1434.482#还可以比较置信区间,方差,...#clogistic可让您检查分析的实际样本量:res.clogis$n[1] 3000
显然,所有数据(30 * 100)都用于估算。这是因为没有一个参与者在所有问题上都得分为零,在所有问题上都得分为1(最低为1,最高为30分中的26分)。所有数据都有助于估计,因此本示例中的方差估计是有效的。
# 联合极大似然估计
标准逻辑回归,请注意使用对比res.jml
前三十个系数(Intercept) item1 item2 item3 item4
-3.688301292 0.052618523 0.811203577 -0.674538589 -1.348580496 item5 item6 item7 item8 item90.102524596 0.706839644 0.758800752 0.553154545 -1.148683041 item10 item11 item12 item13 item14
-0.674538589 0.401891360 -1.566821260 -2.193640539 0.351826379 item15 item16 item17 item18 item19
-0.619482689 0.351826379 -0.097839229 -0.786973625 0.706839644 item20 item21 item22 item23 item240.971562267 1.026247034 0.706839644 0.002613624 -0.844497142 item25 item26 item27 item28 item291.252837340 -0.097839229 -0.301589647 -0.786973625 0.758800752
item29与V30相同。差异是由估算方法的差异引起的。要获得第一个问题V1的难易程度,只需将问题1到问题29的系数求和,然后乘以-1。
sum(coef(res.j[1] 1.625572
# 多层次逻辑回归或MML
我希望回归系数是问题到达时的难易程度,`glmmTMB()`不提供对比选项。我要做的是运行`glmer()`两次,将第一次运行的固定效果和随机效果作为第二次运行的起始值。
# 使用多层次模型复制Rasch结果
提供个体-问题映射:
plot(res.rasch)

要创建此图,我们需要问题难度(回归系数* -1)和个体能力(随机截距)。
* * *
**点击标题查阅往期内容**

[数据分享|PYTHON用PYSTAN贝叶斯IRT模型拟合RASCH模型分析学生考试问题数据](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247515475&idx=1&sn=36c349731ed2140dc6f303f500e02bed&chksm=fd928358cae50a4e68a7a0e51f1ebb11d455309d23daee89b6c6eb08da06b2a44c5478048656&scene=21#wechat_redirect)

左右滑动查看更多

**01**
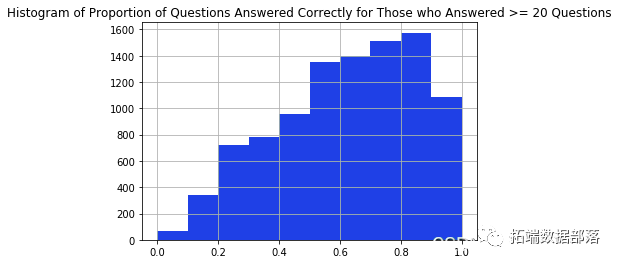
**02**
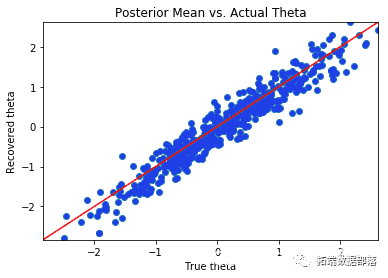
**03**
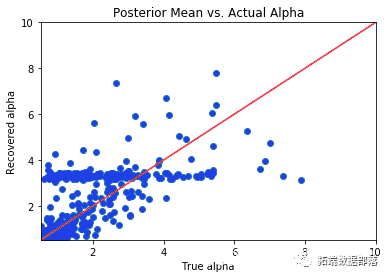
**04**
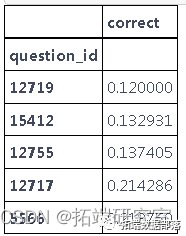

极端的分数是不同的。这归因于MML的差异。由于CML不提供人为因素,因此必须使用两步排序过程。
# 问题特征曲线
问题特征曲线:
plot(res.rasch)

在这里,我们需要能够根据学生的潜能来预测学生正确答题的概率。我所做的是使用逻辑方程式预测概率。获得该数值,就很容易计算预测概率。由于我使用循环来执行此操作,因此我还要计算问题信息,该信息是预测概率乘以1-预测概率。
GGPLOT可视化ggplot(test.info.df, aes(x = theta, y = prob, colour = reorder(item, diff, mean))) +
geom_line() +ct response", colour = "Item",
下面将逐项绘制
ggplot(test.info.df, aes(x = theta, y = prob)) + geom_line() +
scale_x_continuous(breaks = seq(-6, 6, 2), limits = c(-4, 4)) +
scale_y_continuous(labels = percent, breaks = seq(0, 1, .
# 个体参数图
plot(person.parameter(res.rasch))

我们需要估计的个体能力:
ggplot(raschdat1.long, aes(x = tot, y = ability)) +
geom_point(shape = 1, size = 2) + geom_line() +
scale_x_continuous(breaks = 1:26) +
theme_classic()

### 问题均方拟合
对于infit MSQ,执行相同的计算。
eRm:
ggplot(item.fit.df, aes(x = mml, y = cml)) +
scale_x_continuous(breaks = seq(0, 2, .1)) +
scale_y_continuous(breaks = seq(0, 2, .1))

似乎CML的MSQ几乎总是比多层次模型(MML)的MSQ高。
eRm:

来自CML的MSQ几乎总是比来自多层次模型(MML)的MSQ高。我使用传统的临界值来识别不适合的人。
### 测试信息
eRm:
plotINFO(res.rasch)

创建ICC计算测试信息时,我们已经完成了上述工作。对于总体测试信息,我们需要对每个问题的测试信息进行汇总:


最后,我认为使用标准测量误差(SEM),您可以创建一个置信区间带状图。SEM是测试信息的反函数。

该图表明,对于一个估计的能力为-3的个体,他们的能力的估计精度很高,他们的实际分数可能在-1.5和-4.5之间。
经过这一工作,我可以更好地理解该模型,以及其中的一些内容诊断。
* * *

点击文末 **“阅读原文”**
获取全文完整资料。
本文选自《R语言使用Rasch模型分析学生答题能力》。
**点击标题查阅往期内容**
[数据分享|PYTHON用PYSTAN贝叶斯IRT模型拟合RASCH模型分析学生考试问题数据](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247515475&idx=1&sn=36c349731ed2140dc6f303f500e02bed&chksm=fd928358cae50a4e68a7a0e51f1ebb11d455309d23daee89b6c6eb08da06b2a44c5478048656&scene=21#wechat_redirect)
[R语言IRT理论:扩展Rasch模型等级量表模型lltm、 rsm 和 pcm模型分析心理和教育测验数据可视化](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247512660&idx=1&sn=6d5442e0a418b77dd0c8410cc04fca5d&chksm=fd928c5fcae50549e6d4be489633aedfe8d29ffe7f4cc5ea3a732edb99131a3a18ccc6899598&scene=21#wechat_redirect)
[R语言拟合扩展Rasch模型分析试题质量](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247499536&idx=1&sn=dfc544335de110db9938a1f59236d712&chksm=fd92c11bcae5480d5b1cd1860e5ab2eab7ce4a81118de665af0b0e0f2bdb976ee559ab38b030&scene=21#wechat_redirect)
[R语言使用Rasch模型分析学生答题能力](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247494103&idx=2&sn=f69a178617b8fe7fe707b771fbd3bcfe&chksm=fd92d7dccae55ecacf7fec402274112e3a144ce529c8aa0339a28c2a0514c8ca5ecebf6fbe76&scene=21#wechat_redirect)
[R语言中的BP神经网络模型分析学生成绩](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247493916&idx=1&sn=0e791b1a36ee5e0e506511f7961cc3da&chksm=fd92d717cae55e016f5372c9105c6780676c25efad67c3144b423ecf57e1a1b80ef61a47768c&scene=21#wechat_redirect)
[R语言方差分析(ANOVA)学生参加辅导课考试成绩差异](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247491928&idx=1&sn=e3599bde6f64a70dbabfecff690db969&chksm=fd92df53cae55645013bbe6833274f3ade10010e45d10224c776316f5da0fd77401449df3628&scene=21#wechat_redirect)
[数据视域下图书馆话题情感分析](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247490960&idx=2&sn=b306c1e19e92152c79ee405e61f584c2&chksm=fd91239bcae6aa8dbafa98d7ecdbb3880ae65b1769167ee48fe81ede6450e23ed60423baa73f&scene=21#wechat_redirect)
[探析大数据期刊文章研究热点](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247489877&idx=1&sn=736f81cfa82b6ab4e458f38c67861842&chksm=fd91275ecae6ae486d1b1e59ce1db0659bb5fc41f89aaf3c7217f6281d2c836b5450819959a6&scene=21#wechat_redirect)
[R语言LME4混合效应模型研究教师的受欢迎程度](http://mp.weixin.qq.com/s?__biz=MzU4NTA1MDk4MA==&mid=2247493532&idx=2&sn=d030e0d35073fe7522bd644a163a348d&chksm=fd92d997cae55081aa6d55c57278f94b0640c1ee8770046d05d71320948f298a4530ee104864&scene=21#wechat_redirect)
**粗体** _斜体_ [链接](http://example.com) `代码` - 列表 > 引用。你还可以使用@来通知其他用户。