从 0 开始机器学习 - 神经网络识别手写字符!

一、问题描述

今天登龙跟大家分享下使用前馈神经网络识别 10 种类型手写字符的方法，不太了解神经网络基础的同学，可以查看我上一篇文章：从 0 开始机器学习- 深入浅出神经网络基础

我们的目标就是用一个已经训练好的神经网络来预测下面这 10 类手写字符 [0 - 9]：

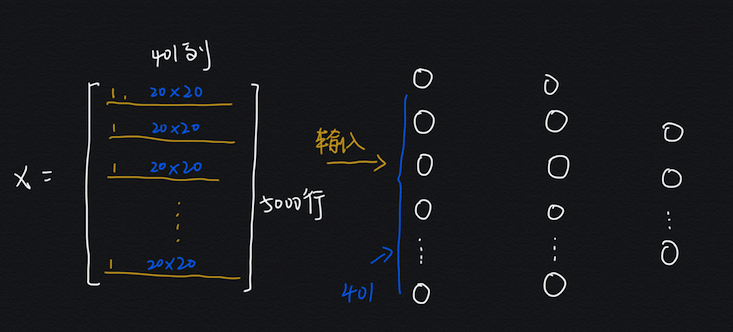
每个字符是一个 20 X 20 = 400 像素的图片：

OK！我们直接开始，先来看看我们用的神经网络的架构。

二、神经网络架构

我们在使用神经网络之前需要进行参数的训练，也就是训练权重矩阵，这篇博客就不详细展开如何训练了，后面单独写一篇反向 BP 算法的文章介绍。

不管是训练还是预测，我们都要首先搞清楚使用的神经网络架构是怎样的，也就是输入输出层有多少节点，有多少个隐藏层，每个隐藏层有多少节点，这些很重要，因为每层的节点数都作为权重矩阵的行和列，在预测的时候要使用这些权重矩阵。

我们这个例子使用的的 3 层神经网络，我来给你详细分析下这个架构：

• 输入层（400）：输入特征为一个 20 x 20 = 400 像素的字符图像，所以有 400 个输入单元，还有一个偏置单元没算在内
• 隐藏层（25）：隐藏层 25 个节点，同样还有一个偏置单元没算在内
• 输出层（10）：因为要分类 10 个数字，所以用 10 个输出表示类别，哪个输出 1 表示识别为哪个数字

结构搞清楚后，我们直接开始预测，下面我带你解析关键的 Python 代码，完整代码见文末 Github 仓库链接。

三、Python 识别手写字符

3.1 加载权重矩阵

我们使用提前训练好的神经网络参数，再提醒一下训练神经网络就是训练每层之间的连接权重，这些连接权重组和起来就是权重矩阵，相邻的 2 层之间有一个权重矩阵，我们就是加载这些矩阵，然后用这些矩阵与输入图像的 400 个像素组成的向量一步步相乘，最终得出一个 1 X 10 的向量表示预测的数字是哪个。

加载权重的代码如下：

# 加载已经训练好的 3 层神经网络参数
def load_weight(path):
    data = sio.loadmat(path)
    return data['Theta1'], data['Theta2']

我们来加载 2 个权重矩阵（因为我们是 3 层神经网络，所以只有 2 个权重矩阵哦）：

# 使用已经训练好的神经网络参数
# 输入层：400，隐藏层：25，输出层：10
theta1, theta2 = load_weight('ex3weights.mat')

theta1.shape, theta2.shape

输入的 2 个权重矩阵的维度分别是：

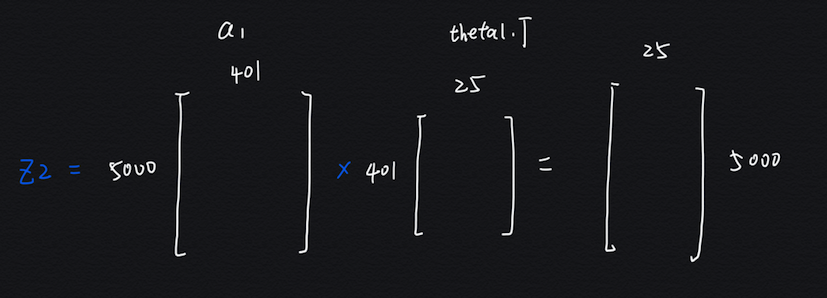
(25, 401), (10, 26)

这符合我们的网络架构：

• theta1 是 25 行 401 列，行数为隐藏层单元数，列数为输入层单元数 + 一个偏置单元
• theta2 是 10 行 26 列，行数为输出层单元数，列数为隐藏层单元数 + 一个偏置单元

如下图：

3.2 开始前馈预测

先加载要识别的手写字符数据：

X, y = load_data('ex3data1.mat', transpose = False)

X.shape, y.shape

输入的 X 是 5000 行 401 列，y 是 5000 行一列，这个数据集我上篇文章有详细介绍过：从 0 开始机器学习 - 逻辑回归识别手写字符！

先定义下每层的输入输出：

• $a$：表示每层神经元的输出，注意是经过 sigmoid 等激活函数运算后的输出
• $z$：表示每层神经元的输入，$a = sigmoid(z)$

首先把输入的特征矩阵直接作为第一层神经元的输出 $a1$，注意虽然这里是把所有的样本一次性输入给神经网络，但是因为是矩阵运算，所以可以理解为每次处理一个样本，也就是特征矩阵的一行：

a1 = X

计算第二层隐藏层的输入 $z2$，注意这里对 theta1 取了转置，是因为矩阵要能够相乘，必须第一个矩阵的列数等于第二个矩阵的行数：

z2 = a1 @ theta1.T

给第二层隐藏层加上偏置单元，也就是增加第一列全 1 向量：

z2 = np.insert(z2, 0, values = np.ones(z2.shape[0]), axis = 1)

计算第二层隐藏层神经元的输出 $，使用 sigmoid 激活函数：

a2 = sigmoid(z2)

再继续利用隐藏层的输出作为最后输出层的输入 $z3$，这里的转置也是为了做矩阵乘法：

z3 = a2 @ theta2.T

计算输出层的输出 $a3$：

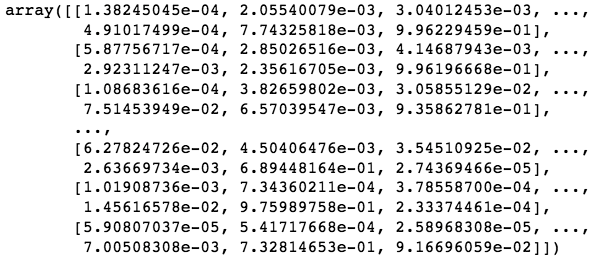
a3 = sigmoid(z3)

这个 $a3$ 就是我们最后对原始手写字符的识别结果，如下：

不过这样不太直观，我们再来取出每行最大值的索引，就是识别的数字：

y_pred = np.argmax(a3, axis = 1) + 1

y_pred

结果如下：

array([10, 10, 10, ...,  9,  9,  9])

第一个 10 表示原数据集第一个书写字符识别为 10，最后一个 9 表示原数据集最后一个手写字符的识别结果，有了识别的结果，我们再来看看总体识别的准确度如何？

来打印下分类报告：

print(classification_report(y, y_pred))

可以看到识别的准确度还是挺高的，能达到 97% 以上！OK！今天登龙就跟大家分享这些，下期再见！

文中的完整可运行代码链接：前馈神经网络预测代码