如图,非常不解这两步是怎么相等的,第一个箭头所指的这个式子是怎么推算到第二个箭头所指的式子的?
学下怎么写公式,思路是楼上的
$$ \frac{1}{n^3}*\frac{(n-1)n(2n-1)}{6} = \frac{(n-1)n(2n-1)}{6*n^3} $$
$$ = \frac{1}{3}*\frac{n-1}{n}*\frac{n}{n}*\frac{2n-1}{2n} = \frac{1}{3}*(1-\frac{1}{n})*1*(1-\frac{1}{2n}) $$
$$ = \frac{1}{3}*(1-\frac{1}{n})*(1-\frac{1}{2n}) $$
撰写回答
你尚未登录,登录后可以
- 和开发者交流问题的细节
- 关注并接收问题和回答的更新提醒
- 参与内容的编辑和改进,让解决方法与时俱进

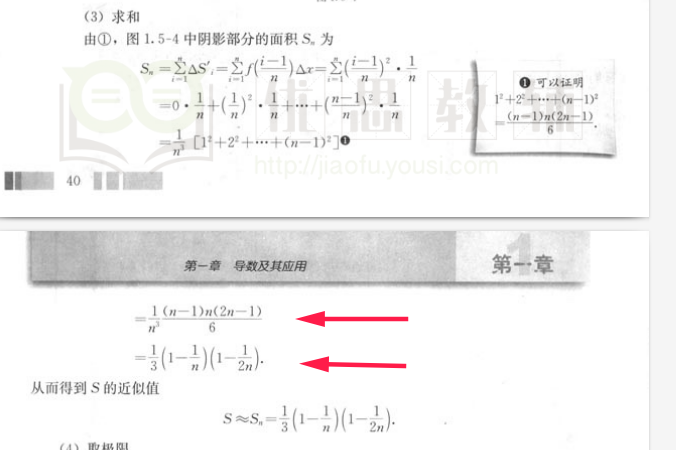
就是把前面那个 1/n^3 分成 3 个 1/n,分别乘以后面分子的三个因子了呀。比如
$$ \frac{1}{n} * (n-1) = 1 - \frac{1}{n} $$